无偿损失 什么是无偿损失 在Uniswap上添加流动性挖矿的时候,由于价格波动,偏离了添加流动性时的价格,会导致一种总资产价值损失。成为无偿损失。这种损失的原因是在Uniswap恒定积机制下代币价格背离产生的。如果价格回归到了添加流动性时的价格,这种损失就会为 0.价格背离越大,损失越大。无论价格上涨或下跌,都会有无常损失。
例如我们添加ETH/DAI的交易对来挖矿。则无论 ETH 价格上涨还是下跌,移除流动性以后,拿到手的 ETH 和 DAI 的总价值会有损失
无偿损失的原因 根据Uniswap恒定积公式,可以做以下推导。
设恒定积为K
tokenA: 数量为a,价格为Pa
tokenB: 数量为b,价格为Pb
根据恒定积公式:
a ∗ b = K a * b = K a ∗ b = K
tokenA的价格: P a = b a Pa = {b \over a} P a = a b
tokenB的价格: P b = a b Pb = {a \over b} P b = b a
{ a ∗ b = K P a = b a = > b = a ∗ P a \begin{cases} a * b = K &\ \\ Pa = {b \over a} => b = a * Pa &\ \end{cases} { a ∗ b = K P a = a b => b = a ∗ P a a = K P a a = \sqrt{K \over Pa} a = P a K
同理
{ a ∗ b = K P a = b a = > a = b P a \begin{cases} a * b = K &\ \\ Pa = {b \over a} => a = {b \over Pa} &\ \end{cases} { a ∗ b = K P a = a b => a = P a b b = K ∗ P a b = \sqrt{K * Pa} b = K ∗ P a
设: 添加流动性时,所占池子比例为 n。当 A 以 B 记价的价格上涨了一个比率 r 后,我们有多大比率的无偿损失
如果不参与挖矿,上涨后,两个代币总价值
当前池子中代币 A 的数量: K P a \sqrt{K \over Pa} P a K
我们占池子的比例是 n,则,我们手里代币 A 的数量为: n K P a n\sqrt{K \over Pa} n P a K n K P a ∗ P a ( r + 1 ) n\sqrt{K \over Pa} * Pa(r+1) n P a K ∗ P a ( r + 1 )
同理:
当前池子中代币 B 的数量: K ∗ P a \sqrt{K * Pa} K ∗ P a n K ∗ P a n\sqrt{K * Pa} n K ∗ P a n K ∗ P a n\sqrt{K * Pa} n K ∗ P a
两个代币的总价值: n K P a ∗ P a ( r + 1 ) + n K ∗ P a n\sqrt{K \over Pa} * Pa(r+1) + n\sqrt{K * Pa} n P a K ∗ P a ( r + 1 ) + n K ∗ P a
如果参与了流动性挖矿,上涨后,两个代币的总价值
上涨后代币 A 的价格: P a ( r + 1 ) Pa(r+1) P a ( r + 1 )
上涨后代币 A 的数量: K P a ( r + 1 ) \sqrt{K \over Pa(r+1)} P a ( r + 1 ) K n P a ( r + 1 ) K P a ( r + 1 ) = > n ( P a ( r + 1 ) ) 2 ∗ K P a ( r + 1 ) = > n K ∗ P a ( r + 1 ) nPa(r+1)\sqrt{K \over Pa(r+1)} => n\sqrt{(Pa(r+1))^2 * {K \over Pa(r+1)}} =>n\sqrt{K * Pa(r+1)} n P a ( r + 1 ) P a ( r + 1 ) K => n ( P a ( r + 1 ) ) 2 ∗ P a ( r + 1 ) K => n K ∗ P a ( r + 1 )
上涨后代币 B 的数量: K ∗ P a ( r + 1 ) \sqrt{K * Pa(r+1)} K ∗ P a ( r + 1 ) n K ∗ P a ( r + 1 ) n\sqrt{K * Pa(r+1)} n K ∗ P a ( r + 1 )
两个代币总价值: n K ∗ P a ( r + 1 ) + n K ∗ P a ( r + 1 ) = 2 n K ∗ P a ( r + 1 ) n\sqrt{K * Pa(r+1)} + n\sqrt{K * Pa(r+1)} = 2n\sqrt{K * Pa(r+1)} n K ∗ P a ( r + 1 ) + n K ∗ P a ( r + 1 ) = 2 n K ∗ P a ( r + 1 )
比较计算无偿损失
通过不参与流动性挖矿和参与流动性挖矿后,两个代币总价值相减得出:
n K P a ∗ P a ( r + 1 ) + n K ∗ P a − 2 n K ∗ P a ( r + 1 ) n\sqrt{K \over Pa} * Pa(r+1) + n\sqrt{K * Pa}-2n\sqrt{K * Pa(r+1)} n P a K ∗ P a ( r + 1 ) + n K ∗ P a − 2 n K ∗ P a ( r + 1 )
=> n K ∗ P a ( r + 1 ) + n K ∗ P a − 2 n K ∗ P a ∗ r + 1 n\sqrt{K*Pa}(r+1) + n\sqrt{K*Pa} - 2n\sqrt{K*Pa} * \sqrt{r+1} n K ∗ P a ( r + 1 ) + n K ∗ P a − 2 n K ∗ P a ∗ r + 1
=> n K ∗ P a ( r + 2 − 2 n r + 1 ) n\sqrt{K*Pa}(r + 2 - 2n\sqrt{r+1}) n K ∗ P a ( r + 2 − 2 n r + 1 )
我们要计算无偿损失率。就拿无偿损失/不添加流动性时的总价值
将不添加流动性时的总价值做一下简化得出:
n K P a ∗ P a ( r + 1 ) + n K ∗ P a n\sqrt{K \over Pa} * Pa(r+1) + n\sqrt{K * Pa} n P a K ∗ P a ( r + 1 ) + n K ∗ P a n K ∗ P a ( r + 2 ) n\sqrt{K * Pa}(r+2) n K ∗ P a ( r + 2 )
计算比率: n K ∗ P a ( r + 2 − 2 n r + 1 ) n K ∗ P a ( r + 2 ) n\sqrt{K*Pa}(r + 2 - 2n\sqrt{r+1}) \over n\sqrt{K * Pa}(r+2) n K ∗ P a ( r + 2 ) n K ∗ P a ( r + 2 − 2 n r + 1 ) r + 2 − 2 n r + 1 r + 2 r+2-2n\sqrt{r+1} \over r+2 r + 2 r + 2 − 2 n r + 1
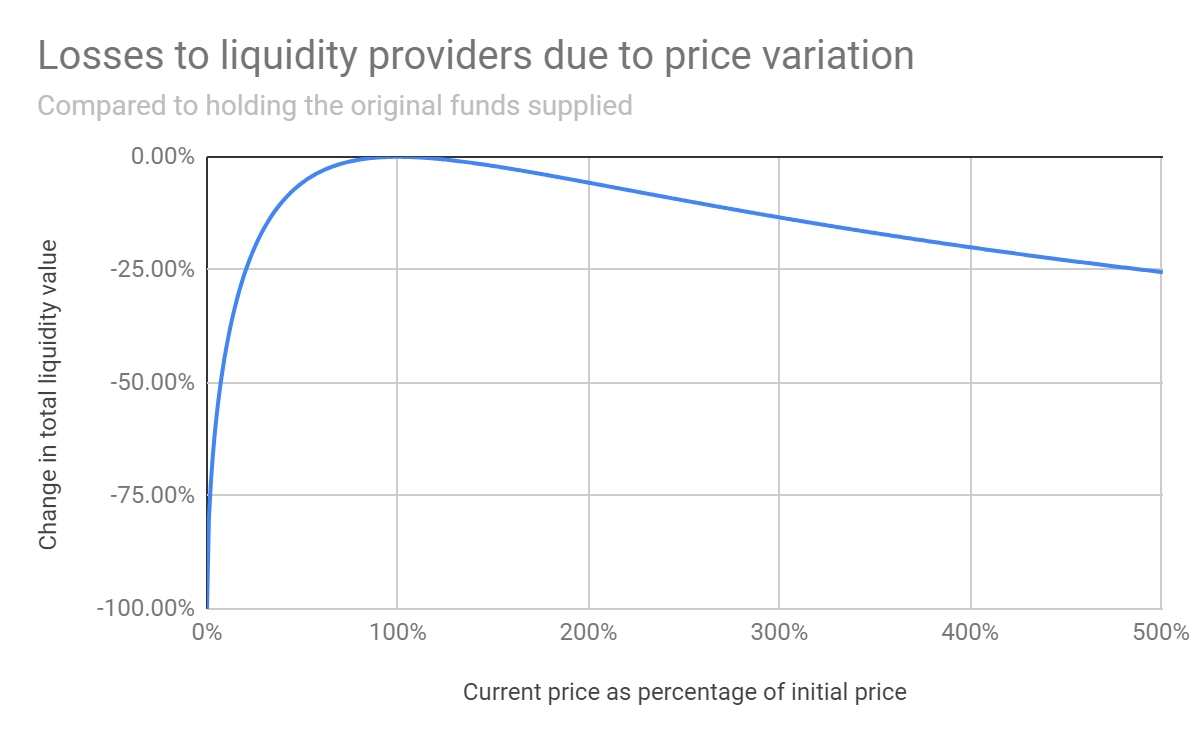
所以可以看出,无偿损失率只与波动率有关。与上涨下跌无关。Uniswap官方给出的损失模型如下
或者换一种说法:
相对于 HODL,1.25 倍的价格变化导致 0.6% 的损失 相对于 HODL,1.50 倍的价格变化导致 2.0% 的损失 相对于 HODL,1.75 倍的价格变化导致 3.8% 的损失 相对于 HODL,2 倍的价格变化导致 5.7% 的损失 相对于 HODL,3 倍的价格变化导致 13.4% 的损失 相对于 HODL,4 倍的价格变化导致 20.0% 的损失 5 倍的价格变化导致相对于 HODL 损失 25.5% 注意 ,无论价格变化发生在哪个方向,损失都是相同的(即价格翻倍导致与减半相同的损失)。
参考资料